Unveiling the Essence of Linear Transformations: A Comprehensive Exploration

Related Articles: Unveiling the Essence of Linear Transformations: A Comprehensive Exploration

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Essence of Linear Transformations: A Comprehensive Exploration. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Essence of Linear Transformations: A Comprehensive Exploration

In the realm of mathematics, particularly within the fields of linear algebra and abstract algebra, the concept of a linear transformation holds a paramount position. It serves as a fundamental building block for understanding and manipulating vector spaces, which are mathematical structures that generalize the familiar notions of points, lines, and planes in Euclidean space.

This article delves into the intricacies of linear transformations, providing a comprehensive understanding of their definition, properties, and significance. We will explore how these transformations preserve the fundamental operations of vector addition and scalar multiplication, thereby preserving the inherent structure of vector spaces.

Defining Linear Transformations: A Bridge Between Vector Spaces

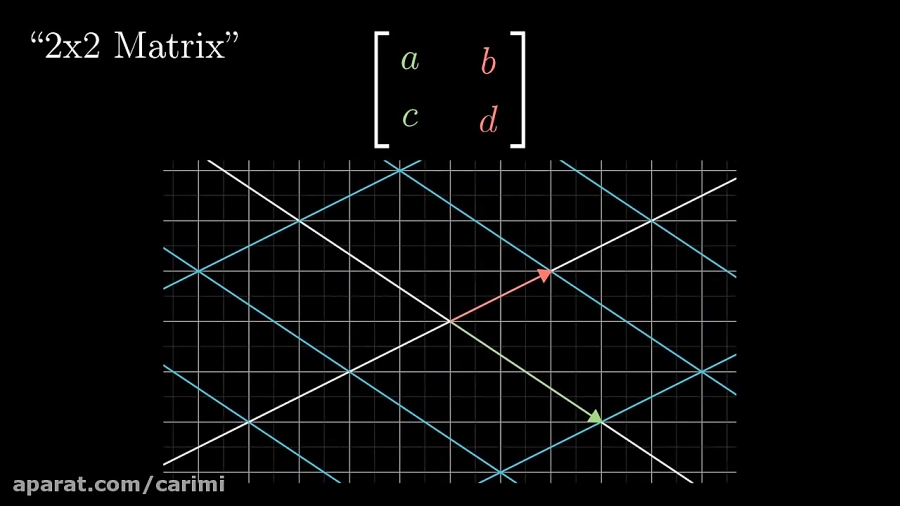
At its core, a linear transformation is a function that maps vectors from one vector space to another, while adhering to specific rules that ensure the preservation of the underlying vector space structure. Formally, a linear transformation T from a vector space V to a vector space W, denoted as T: V → W, satisfies the following conditions:

1. Additivity: For any vectors u and v in V, T(u + v) = T(u) + T(v).
2. Homogeneity: For any scalar c and vector v in V, T(cv) = c T(v).

These two conditions encapsulate the essence of a linear transformation. They dictate that the transformation preserves the operations of vector addition and scalar multiplication. This preservation of structure is crucial for many applications, as it allows us to analyze and manipulate vectors in a consistent manner across different vector spaces.

Illustrative Examples: Bringing Linear Transformations to Life

To grasp the concept of linear transformations more concretely, consider the following examples:

• Rotation in Two Dimensions: Imagine a transformation that rotates all vectors in a two-dimensional plane by a fixed angle. This transformation is linear, as it preserves both vector addition (rotating the sum of two vectors is equivalent to rotating each vector individually and then adding the results) and scalar multiplication (rotating a vector scaled by a factor is the same as scaling the rotated vector by the same factor).

• Scaling in Three Dimensions: Consider a transformation that scales all vectors in three-dimensional space by a constant factor. This transformation is also linear, as it preserves both vector addition and scalar multiplication.

• Projection onto a Line: A transformation that projects vectors onto a specific line in space is another example of a linear transformation. This transformation preserves vector addition and scalar multiplication, as the projection of the sum of two vectors is the sum of their projections, and the projection of a scaled vector is the scaled projection of the original vector.

These examples highlight the diverse nature of linear transformations and their ability to represent various geometric operations while maintaining the fundamental structure of vector spaces.

Properties of Linear Transformations: Unlocking their Potential

Linear transformations possess several key properties that make them particularly useful in mathematics and its applications:

• Kernel and Image: Every linear transformation has an associated kernel, which is the set of all vectors in the domain that are mapped to the zero vector in the codomain. The kernel provides insights into the null space of the transformation. Additionally, every linear transformation has an associated image, which is the set of all vectors in the codomain that are the image of some vector in the domain. The image represents the range of the transformation.

• Invertibility: A linear transformation is invertible if and only if its kernel contains only the zero vector. In this case, there exists an inverse transformation that maps vectors from the codomain back to the domain, effectively reversing the original transformation.

• Linear Independence: Linear transformations preserve linear independence. If a set of vectors is linearly independent in the domain, its image under a linear transformation will also be linearly independent in the codomain.

• Basis Transformation: Linear transformations can be used to change the basis of a vector space. This allows us to represent vectors in different coordinate systems, which can be advantageous for solving certain problems.

These properties highlight the power and versatility of linear transformations, allowing them to play a crucial role in various mathematical and scientific disciplines.

Applications of Linear Transformations: Bridging Theory and Practice

Linear transformations find applications in numerous fields, including:

• Computer Graphics: Linear transformations are extensively used in computer graphics to perform operations such as rotation, scaling, and translation of objects.

• Linear Programming: In optimization problems, linear transformations are used to represent constraints and objective functions, allowing for efficient solutions.

• Quantum Mechanics: In quantum mechanics, linear transformations are used to describe the evolution of quantum states, providing a framework for understanding the behavior of particles at the atomic and subatomic levels.

• Signal Processing: Linear transformations are employed in signal processing to filter and analyze signals, enabling the extraction of meaningful information from complex data.

• Machine Learning: Linear transformations are fundamental to various machine learning algorithms, such as linear regression and support vector machines, where they are used to project data into higher-dimensional spaces for better classification and prediction.

These applications underscore the broad impact of linear transformations, demonstrating their ability to bridge theoretical concepts with practical applications across diverse domains.

FAQs: Addressing Common Queries about Linear Transformations

1. What is the difference between a linear transformation and a general function?

A linear transformation is a specific type of function that satisfies the additivity and homogeneity properties. General functions do not necessarily adhere to these conditions.

2. How do I determine if a given function is a linear transformation?

To determine if a function is a linear transformation, verify whether it satisfies the additivity and homogeneity properties. If it does, then it is a linear transformation.

3. What is the significance of the kernel and image of a linear transformation?

The kernel provides information about the null space of the transformation, indicating vectors that are mapped to the zero vector. The image represents the range of the transformation, showing the set of vectors that can be obtained as outputs.

4. How can I represent a linear transformation mathematically?

Linear transformations can be represented using matrices. The matrix representation allows for efficient computation of the transformation of vectors.

5. How are linear transformations used in real-world applications?

Linear transformations are used in diverse applications, including computer graphics, optimization, quantum mechanics, signal processing, and machine learning.

Tips for Understanding Linear Transformations

• Visualize: Use geometric interpretations to understand the effects of linear transformations on vectors.
• Focus on Properties: Understand the key properties of linear transformations, such as additivity, homogeneity, kernel, and image.
• Practice Examples: Work through examples to solidify your understanding of the concepts.
• Connect with Applications: Explore how linear transformations are used in various fields to gain a deeper appreciation for their practical significance.

Conclusion: Embracing the Power of Linear Transformations

Linear transformations are a fundamental concept in mathematics with far-reaching applications. Their ability to preserve the structure of vector spaces while enabling diverse operations makes them indispensable tools in various fields. By understanding their definition, properties, and applications, we can unlock their full potential and leverage their power to solve complex problems across diverse disciplines. As we delve deeper into the world of mathematics and its applications, the concept of linear transformations will undoubtedly continue to play a pivotal role in shaping our understanding of the world around us.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Essence of Linear Transformations: A Comprehensive Exploration. We appreciate your attention to our article. See you in our next article!